Matematyka jest królową nauk, czemu zapewne nikt nie zaprzeczy. Na maturze może zdarzyć się sytuacja, w której konieczne będzie obliczenie wartości stężenia molowego kationów wodoru na podstawie wartości pH, która nie będzie liczbą naturalną. I odwrotnie – wymagane będzie obliczenie wartości pH na podstawie znajomości stężenia molowego jonów H⁺. Wasz prosty kalkulator, zawierający jedynie podstawowe funkcje działań na liczbach nie będzie w stanie wykonać takich obliczeń. W takiej sytuacji nie jesteście jednak bezbronni, ponieważ podczas egzaminu maturalnego będziecie mieć pod ręką tablice logarytmiczne 😉 Dziś pokażę Wam, w jaki sposób należy z nich wówczas skorzystać. Zapraszam serdecznie do zapoznania się z tym poradnikiem. Podczas rozwiązania zadań z poniższych przykładów posłużymy się tablicą wartości logarytmów dziesiętnych, której fragment został zamieszczony w poniższej tabeli^*:

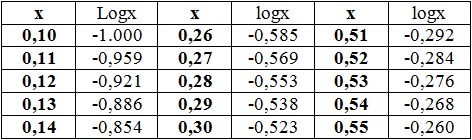
^*Dane liczbowe pochodzą z karty wybranych wzorów i stałych fizykochemicznych na egzamin maturalny z biologii, chemii i fizyki opracowanej przez Centralną Komisję Egzaminacyjną.

 

Przykład 1: oblicz wartość pH roztworu, w którym stężenie kationów wodoru równe jest 0,27 mol∙dm^-3.

Wiemy, że pH = -log[H⁺], zatem pH = -log(0,27). Ponieważ wartość liczbowa 0,27 nie jest wielokrotnością liczby 10, wartość takiego działania logarytmowania należy odczytać z tablic. W naszym przypadku X = 0,27, zatem logX odpowiada wartości równej 0,569 (niebieski prostokąt w kolumnie logX w tabeli):

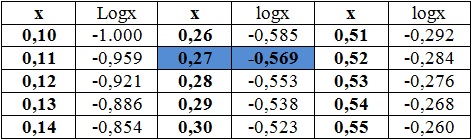
Stąd pH = 0,569.

 

Przykład 2: oblicz wartość pH roztworu, w którym stężenie jonów wodorowych równe jest 0,0055 mol∙dm^-3.

Ponieważ dla zapisu pH = -log(0,0055) nie jesteśmy w stanie odnaleźć odpowiedniej wartości logarytmu w tablicach, liczbę logarytmowaną 0,0055 należy zapisać w notacji wykładniczej: pH = -log(0,55·10^-2). Następnie korzystamy z prawa działań na logarytmach, czyli logarytmu z iloczynu liczb:

log(a·b) = log(a) + log(b)

Możemy zatem zapisać, że pH = -[log(0,55) + log(10^-2)]. Wartość wyniku działania log(0,55) odczytana z tablic równa jest  -0,26 (zielony prostokąt w kolumnie logX w tabeli):

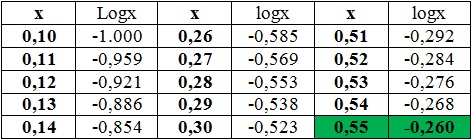
Wartość wyniku działania log(10^-2) równa jest -2 (czyli wykładnikowi potęgi liczby logarytmowanej). Obie wartości wstawiamy do naszego równania i obliczamy:

pH = -[-0,26-2]. Stąd pH = 2,26.

 

Przykład 3: oblicz stężenie molowe jonów wodorowych w roztworze, którego pH = 2,9.

Wiemy, że [H⁺] = 10^-pH, zatem możemy zapisać [H⁺] = 10^-2,9. Ponieważ wartości liczbowej -2,9 nie ma w tablicach logarytmicznych, musimy zapisać ją jako sumę dwóch liczb ujemnych, a dokładnie: -2 – 0,9. Korzystając z prawa działań na potęgach:

a^(b+c) = a^b · a^c

możemy zapisać, że [H⁺] = 10^-2,9 = 10^-2-0,9 = 10^-2 · 10^-0,9. Teraz liczymy wartość liczbową działania 10^-0,9. Aby tego dokonać należy rozwiązać równanie 10^-0,9 = X. Rozwiązujemy je korzystając z własności logarytmu dziesiętnego, zatem możemy zapisać, że -0,9 = logX. W tablicy logarytmów, w kolumnie logX szukamy wartości możliwie najbliższej liczbie -0,9. Jest nią liczba -0,886 (pomarańczowy prostokąt w kolumnie logX w tabeli):

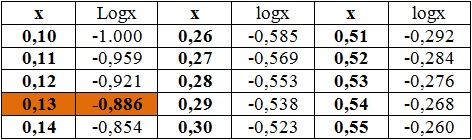
Następnie odczytujemy odpowiadającą jej wartość, którą jest liczba 0,13 (pomarańczowy prostokąt w kolumnie X w tabeli). Stąd rozwiązaniem równania -0,9 = logX jest liczba 0,13. Odczytaną wartość 0,13 wstawiamy do naszego równania [H⁺] = 10^-2· 10^-0,9 za liczbę 10^-0,9 i wówczas [H⁺] = 10^-2· 0,13 = 0,0013. Stąd stężenie molowe jonów H⁺ dla pH = 2,9 wynosi 0,0013 mol∙dm^-3. Dla porównania – wynik obliczeń uzyskany z wykorzystaniem kalkulatora wynosi 0,00126 mol∙dm^-3.

Mam nadzieję, że teraz już nie będziesz mieć problemów z obliczeniami chemicznymi, w których wykorzystuje się tablice logarytmiczne. Zadania związane z tym tematem znajdziesz tutaj.

Spodobał Ci się ten artykuł? Polub mój fanpage na Facebooku oraz na Instagramie, aby nie ominęły Cię żadne nowości.

© dr inż. Rafał Szczypiński, wszelkie prawa zastrzeżone