Wpływ temperatury na szybkość reakcji tłumaczy się wykładniczym wzrostem wartości stałej szybkości reakcji 𝑘. Tę zależność opisuje równanie Arrheniusa:
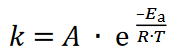
gdzie 𝐸a oznacza energię aktywacji, 𝑅 – uniwersalną stałą gazową, a 𝑇 – temperaturę bezwzględną wyrażoną w kelwinach. Czynnik:
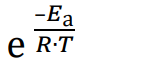
informuje o tym, jaka część zderzających się molekuł ma energię większą lub równą energii aktywacji, natomiast czynnik 𝐴, nazywany czynnikiem przedwykładniczym, określa częstotliwości zderzeń efektywnych. Wartość czynnika 𝐴 jest w praktyce niezależna od temperatury. Równanie Arrheniusa może być przekształcone do postaci logarytmicznej:
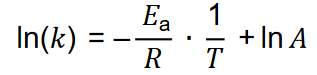
będącej równaniem liniowym (𝑦 = 𝑎𝑥 + 𝑏), opisującym zależność logarytmu naturalnego ze stałej szybkości reakcji ln(𝑘) od odwrotności temperatury (1/𝑇). Wartość
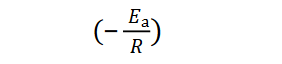
jest współczynnikiem kierunkowym tej prostej.
Badano przebieg reakcji chemicznej, zachodzącej między wodorem i chlorkiem bromu, przebiegającej według następującego równania reakcji:
H2(g) + 2BrCl(g) → Br2(g) + 2HCl(g)
Po ustaleniu mechanizmu opisanej reakcji określono jej równanie kinetyczne jako:
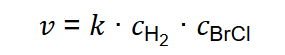
Tę reakcję przeprowadzano w różnych temperaturach należących do przedziału od 310 K do 380 K i za każdym razem wyznaczono wartość jej stałej szybkości. Otrzymane dane zestawiono w tabeli.
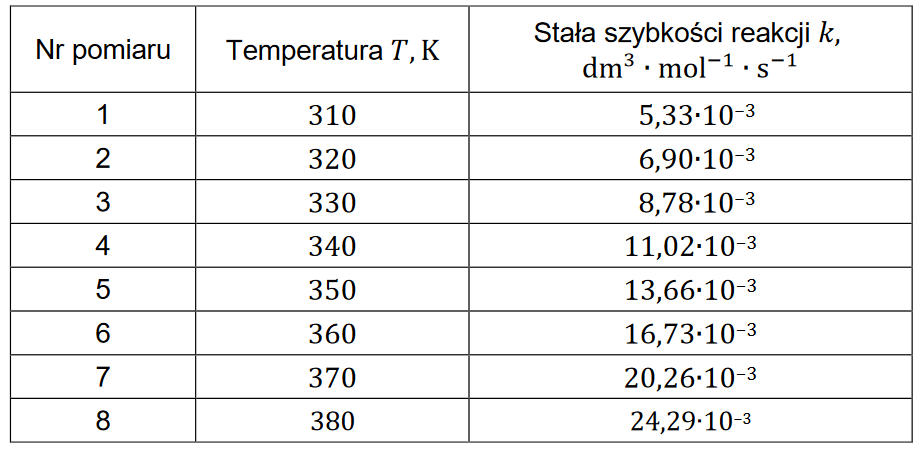
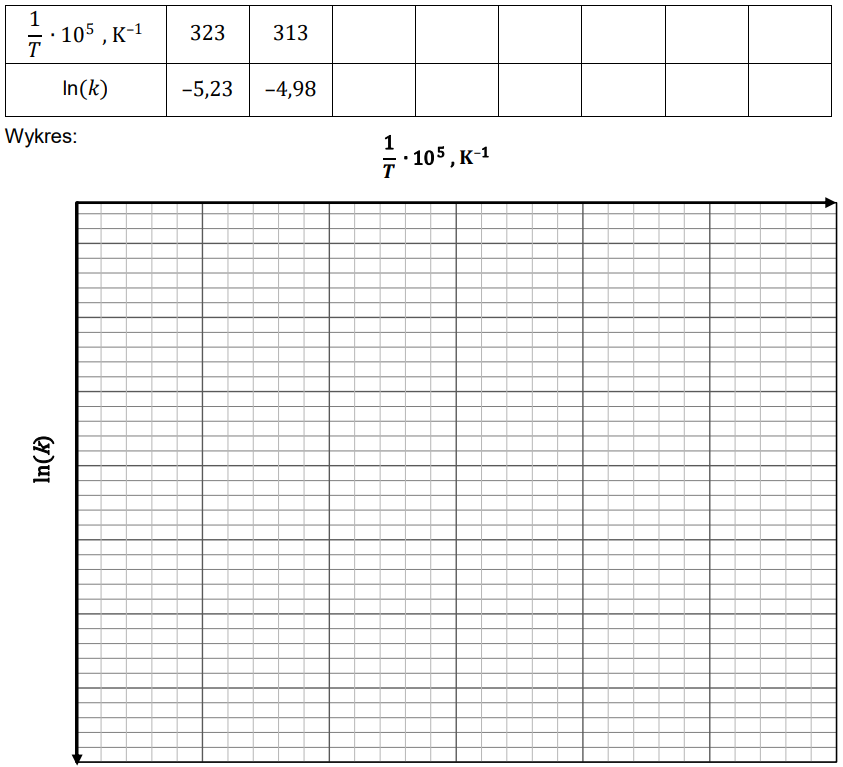
UWAGA: logarytm (ln) o podstawie równej liczbie Eulera, wynoszącej e ≈ 2,7183, podlega takim samym regułom działań jak pozostałe logarytmy o innych podstawach należących do zbioru liczb rzeczywistych.
Uzupełnij tabelę brakującymi wartościami ln(𝒌) (z dokładnością do dwóch miejsc po przecinku) oraz narysuj wykres zależności logarytmu naturalnego ze stałej szybkości reakcji pomiędzy wodorem a chlorkiem bromu ln(𝒌) od odwrotności temperatury (1/T). Następnie oblicz wartość energii aktywacji tej reakcji.
Rozwiązanie tego zadania dostępne jest nieodpłatnie pod poniższym linkiem: