Określanie symboli pierwiastków chemicznych oraz najwyższych stopni utlenienia i liczby elektronów niesparowanych. Zadanie 1.1. Arkusz CKE chemia maj 2024 rozszerzony (2 punkty)
Pierwiastki A i X leżą w sąsiednich okresach. Wiadomo, że:
• elektrony w atomie A w stanie podstawowym są rozmieszczone w pięciu podpowłokach
• w atomie X w stanie podstawowym wszystkie elektrony biorące udział w tworzeniu wiązań są niesparowane i rozmieszczone na powłokach opisanych różnymi wartościami głównej liczby kwantowej 𝑛.
Cząsteczka tlenku pierwiastka A na najwyższym stopniu utlenienia składa się z czternastu atomów, a jej wzór rzeczywisty nie jest wzorem elementarnym. Ten tlenek w reakcji z wodą – przebiegającej bez zmiany stopni utlenienia – tworzy trójprotonowy kwas tlenowy. Liczba atomów wchodzących w skład cząsteczki wodorku pierwiastka A jest równa liczbie atomów wchodzących w skład cząsteczki tlenku pierwiastka X na najwyższym stopniu utlenienia.
Uzupełnij tabelę. Napisz symbole pierwiastków A i X – oraz dla każdego z nich – najwyższy stopień utlenienia w związkach chemicznych i liczbę elektronów niesparowanych w atomie w stanie podstawowym.
Uzupełnienie schematu klatkowego konfiguracji elektronowej. Zadanie 1.2. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Pierwiastki A i X leżą w sąsiednich okresach. Wiadomo, że:
• elektrony w atomie A w stanie podstawowym są rozmieszczone w pięciu podpowłokach
• w atomie X w stanie podstawowym wszystkie elektrony biorące udział w tworzeniu wiązań są niesparowane i rozmieszczone na powłokach opisanych różnymi wartościami głównej liczby kwantowej 𝑛.
Cząsteczka tlenku pierwiastka A na najwyższym stopniu utlenienia składa się z czternastu atomów, a jej wzór rzeczywisty nie jest wzorem elementarnym. Ten tlenek w reakcji z wodą – przebiegającej bez zmiany stopni utlenienia – tworzy trójprotonowy kwas tlenowy. Liczba atomów wchodzących w skład cząsteczki wodorku pierwiastka A jest równa liczbie atomów wchodzących w skład cząsteczki tlenku pierwiastka X na najwyższym stopniu utlenienia.
Uzupełnij poniższy schemat, tak aby przedstawiał graficzny (klatkowy) zapis konfiguracji elektronowej kationu X3+ w stanie podstawowym. W zapisie uwzględnij numery powłok i symbole podpowłok.
Zapis wzorów sumarycznych wodorku oraz tlenków i równań reakcji chemicznych. Zadanie 1.3. Arkusz CKE chemia maj 2024 rozszerzony (3 punkty)
Pierwiastki A i X leżą w sąsiednich okresach. Wiadomo, że:
• elektrony w atomie A w stanie podstawowym są rozmieszczone w pięciu podpowłokach
• w atomie X w stanie podstawowym wszystkie elektrony biorące udział w tworzeniu wiązań są niesparowane i rozmieszczone na powłokach opisanych różnymi wartościami głównej liczby kwantowej 𝑛.
Cząsteczka tlenku pierwiastka A na najwyższym stopniu utlenienia składa się z czternastu atomów, a jej wzór rzeczywisty nie jest wzorem elementarnym. Ten tlenek w reakcji z wodą – przebiegającej bez zmiany stopni utlenienia – tworzy trójprotonowy kwas tlenowy. Liczba atomów wchodzących w skład cząsteczki wodorku pierwiastka A jest równa liczbie atomów wchodzących w skład cząsteczki tlenku pierwiastka X na najwyższym stopniu utlenienia.
Uzupełnij tabelę i napisz równania reakcji: Równanie reakcji 1.: Równanie reakcji 2.:
• w formie cząsteczkowej – tlenku pierwiastka A na najwyższym stopniu utlenienia z wodą (reakcja 1.)
• w formie jonowej – tlenku pierwiastka X na najwyższym stopniu utlenienia z wodorotlenkiem potasu (reakcja 2.).
Użyj symboli A i X.
Zapis symbolu izotopu pierwiastka powstającego w wyniku przemiany beta minus. Zadanie 2.1. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Znanych jest kilkadziesiąt izotopów galu, które powstają w różnych reakcjach jądrowych, ale tylko nieliczne z nich są trwałe. Promieniotwórcze izotopy galu zwykle ulegają rozpadowi 𝛽– , jeżeli mają nadmiar neutronów, lub innym przemianom – przy niedomiarze neutronów.
Izotop galu o liczbie masowej równej 72 ulega rozpadowi 𝛽–.
Uzupełnij poniższy schemat. Wpisz symbol pierwiastka, którego izotop powstaje w wyniku opisanej przemiany, oraz liczbę masową tego izotopu.
Zapis równania przemiany jądrowej. Zadanie 2.2. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Znanych jest kilkadziesiąt izotopów galu, które powstają w różnych reakcjach jądrowych, ale tylko nieliczne z nich są trwałe. Promieniotwórcze izotopy galu zwykle ulegają rozpadowi 𝛽– , jeżeli mają nadmiar neutronów, lub innym przemianom – przy niedomiarze neutronów.
Izotop 67Ga otrzymuje się w wyniku bombardowania izotopu cynku 68Zn pewnymi cząstkami. W reakcji jednego jądra 68Zn z jedną taką cząstką powstają dwa neutrony i jedno jądro 67Ga.
Napisz równanie opisanej przemiany, której ulega jądro izotopu 68Zn. Uzupełnij wszystkie pola w poniższym schemacie.
Wybór właściwych określeń związanych z energią sieciową oraz temperaturą topnienia dwóch związków chemicznych. Zadanie 3. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Energia sieciowa związków jonowych to ilość energii potrzebna do rozłożenia jednego mola krystalicznej substancji na jony leżące nieskończenie daleko od siebie. Jej wartość zależy od rozmiarów jonów i ich ładunków. Wraz ze wzrostem energii sieciowej rosną wartości temperatury topnienia substancji krystalicznych. W tabeli przedstawiono wartości energii sieciowej halogenków wybranych litowców.
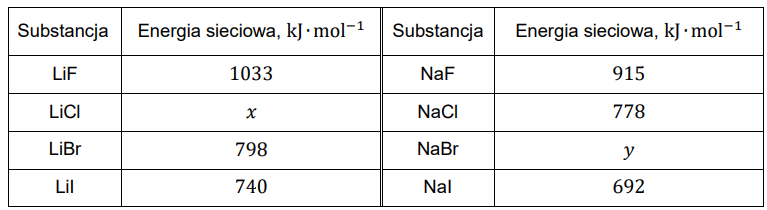
Na podstawie: A. Bielański, Podstawy chemii nieorganicznej, Warszawa 2018.
Uzupełnij poniższe zdania. Wybierz i zaznacz jedną odpowiedź spośród podanych w każdym nawiasie. Energia sieciowa 𝑥 chlorku litu wynosi około (640 / 740 / 840) kJ∙mol–1, a energia sieciowa 𝑦 bromku sodu wynosi około (640 / 740 / 840) kJ∙mol–1. Temperatura topnienia chlorku sodu jest równa 801 °C, a temperatura topnienia jodku sodu jest równa (662 / 882) °C.
Wyjaśnienie przyczyny różnic energii sieciowej MgO oraz LiF. Zadanie 4. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Energia sieciowa związków jonowych to ilość energii potrzebna do rozłożenia jednego mola krystalicznej substancji na jony leżące nieskończenie daleko od siebie. Jej wartość zależy od rozmiarów jonów i ich ładunków. Wraz ze wzrostem energii sieciowej rosną wartości temperatury topnienia substancji krystalicznych. W tabeli przedstawiono wartości energii sieciowej halogenków wybranych litowców.

W poniższej tabeli przedstawiono wartości energii sieciowej dwóch związków oraz promieni tworzących je jonów.

Na podstawie: A. Bielański, Podstawy chemii nieorganicznej, Warszawa 2018.
Wyjaśnij, dlaczego – mimo zbliżonych rozmiarów jonów – energia sieciowa tlenku magnezu różni się znacznie od energii sieciowej fluorku litu.
Wybór właściwych określeń dotyczących struktur krystalicznych tlenku germanu(IV). Zadanie 5. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Liczba koordynacyjna to liczba najbliższych atomów lub jonów otaczających dany atom lub jon w sieci krystalicznej kryształu. Tlenek germanu(IV) jest krystalicznym ciałem stałym. Istnieje w dwóch odmianach: alfa, α-GeO2, oraz beta, β-GeO2. Fragmenty struktur obu odmian przedstawiono poniżej (atomy Ge – szare, atomy O – czerwone).
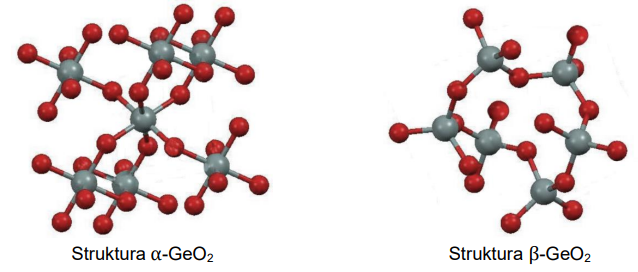
Uzupełnij zdania. Wybierz i zaznacz jedną odpowiedź spośród podanych w każdym nawiasie. W odmianie α-GeO2 liczba koordynacyjna dla atomu germanu wynosi (dwa / cztery / sześć). W strukturze odmiany β-GeO2 dla orbitali walencyjnych atomu germanu zakłada się
hybrydyzację (sp2 / sp3).
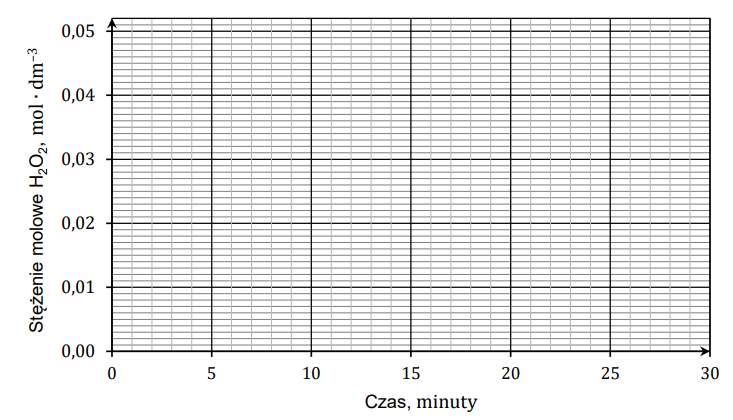
Rysowanie wykresu ilustrującego zmiany stężenia nadtlenku wodoru w próbce. Zadanie 6.1. Arkusz CKE chemia maj 2024 rozszerzony (2 punkty)
Nadtlenek wodoru jest to substancja nietrwała, którą należy przechowywać w zimnym i ciemnym miejscu, gdyż w innych warunkach ulega powolnemu rozkładowi. Postęp rozkładu nadtlenku wodoru można badać np. za pomocą techniki miareczkowania. W termostatowanym naczyniu umieszczono roztwór H2O2 o pewnym stężeniu, który utrzymywano w temperaturze 40 °C. W równych odstępach czasowych z tego roztworu pobierano próbki, które schładzano i miareczkowano za pomocą zakwaszonego roztworu manganianu(VII) potasu o stężeniu 0,0020 mol∙dm−3. Podczas miareczkowania zachodziła reakcja opisana równaniem:
2KMnO4 + 5H2O2 + 3H2SO4 → 2MnSO4 + 5O2 + K2SO4 + 8H2O
Wyznaczenie objętości zużytego roztworu KMnO4 pozwoliło obliczyć stężenie molowe H2O2 w próbce. Objętość każdej pobieranej próbki była równa 2,0 cm3. Uzyskane wyniki przedstawiono w tabeli.

Uzupełnij poniższą tabelę, a następnie narysuj wykres przedstawiający zależność stężenia nadtlenku wodoru od czasu. Wartość stężenia zapisz w zaokrągleniu do trzeciego miejsca po przecinku.
Wybór właściwych określeń dotyczących szybkości reakcji rozkładu nadtlenku wodoru. Zadanie 6.2. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Nadtlenek wodoru jest to substancja nietrwała, którą należy przechowywać w zimnym i ciemnym miejscu, gdyż w innych warunkach ulega powolnemu rozkładowi. Postęp rozkładu nadtlenku wodoru można badać np. za pomocą techniki miareczkowania. W termostatowanym naczyniu umieszczono roztwór H2O2 o pewnym stężeniu, który utrzymywano w temperaturze 40 °C. W równych odstępach czasowych z tego roztworu pobierano próbki, które schładzano i miareczkowano za pomocą zakwaszonego roztworu manganianu(VII) potasu o stężeniu 0,0020 mol∙dm−3. Podczas miareczkowania zachodziła reakcja opisana równaniem:
2KMnO4 + 5H2O2 + 3H2SO4 → 2MnSO4 + 5O2 + K2SO4 + 8H2O
Wyznaczenie objętości zużytego roztworu KMnO4 pozwoliło obliczyć stężenie molowe H2O2 w próbce. Objętość każdej pobieranej próbki była równa 2,0 cm3. Uzyskane wyniki przedstawiono w tabeli.

Uzupełnij zdania. Wybierz i zaznacz jedną odpowiedź spośród podanych w każdym nawiasie. Szybkość reakcji rozkładu nadtlenku wodoru wraz z upływem czasu (rośnie / maleje / nie ulega zmianie).
Szybkość reakcji rozkładu nadtlenku wodoru w temperaturze 40 °C jest (większa niż / mniejsza niż / taka sama jak) w temperaturze 20 °C.
Obliczanie objętości roztworu wodorotlenku baru wprowadzonego do roztworu kwasu solnego. Zadanie 7. Arkusz CKE chemia maj 2024 rozszerzony (2 punkty)
Reakcja kwasu solnego z wodorotlenkiem baru przebiega zgodnie z równaniem:
H3O+ + OH– → 2H2O
Oblicz, ile cm3 wodnego roztworu wodorotlenku baru o stężeniu molowym równym 0,020 mol∙dm–3 należy dodać do 25 cm3 kwasu solnego o pH = 1,5, aby otrzymany roztwór miał pH równe 3,7. Przyjmij, że objętość powstałego roztworu jest sumą objętości użytych roztworów.
Określanie czy strąci się osad w wyniku zmieszania dwóch wodnych roztworów soli. Zadanie 8. Arkusz CKE chemia maj 2024 rozszerzony (2 punkty)
Zmieszano równe objętości dwóch wodnych roztworów: azotanu(V) srebra(I) o stężeniu c1 = 1∙10−4 mol∙dm−3 i chlorku potasu o stężeniu c2 = 2∙10−6 mol∙dm−3. Podczas doświadczenia utrzymywano temperaturę równą 25 oC.
Uzupełnij poniższe zdania. Wpisz wartość iloczynu stężeń kationów srebra(I) i anionów chlorkowych po zmieszaniu roztworów oraz wybierz i zaznacz jedną odpowiedź spośród podanych w każdym nawiasie. Iloczyn stężeń kationów srebra(I) i anionów chlorkowych w otrzymanej mieszaninie jest równy: . Jego wartość jest (mniejsza / większa) od wartości iloczynu rozpuszczalności chlorku srebra(I), dlatego osad tej soli się (nie wytrąci / wytrąci).
Przypisywanie zawartości probówek do wodnych roztworów odpowiednich soli. Zadanie 9.1. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Zbadano odczyn wodnych roztworów trzech soli: NaHCO3, ZnCl2 i CH3COONH4 za pomocą uniwersalnych papierków wskaźnikowych. Wyniki doświadczenia pokazano na zdjęciu.

Uzupełnij tabelę. Przyporządkuj numery probówek do wzorów badanych soli.
Ocena poprawności zdań dotyczących procesów przebiegających w wodnych roztworach soli. Zadanie 9.2. Arkusz CKE chemia maj 2024 rozszerzony (1 punkt)
Zbadano odczyn wodnych roztworów trzech soli: NaHCO3, ZnCl2 i CH3COONH4 za pomocą uniwersalnych papierków wskaźnikowych. Wyniki doświadczenia pokazano na zdjęciu.

Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. 1. W roztworze znajdującym się w probówce 1. reakcji z wodą uległy aniony, a w roztworze, który umieszczono w probówce 3., reakcji z wodą uległy kationy. 2. W roztworze, który umieszczono w probówce 2., reakcji z wodą uległy zarówno kationy, jak i aniony.
Obliczanie stężenia procentowego chlorku manganu(II) w wodnym roztworze powstałym z udziałem hydratu. Zadanie 10. Arkusz CKE chemia maj 2024 rozszerzony (2 punkty)
W 150 cm3 wodnego roztworu chlorku manganu(II) o stężeniu molowym 𝑐 = 0,678 mol∙dm−3 i gęstości 𝑑 = 1,07 g∙cm−3 rozpuszczono 6,00 g hydratu tej soli o wzorze MnCl2∙4H2O.
Na podstawie: Z. Dobkowska, K.M. Pazdro, Szkolny poradnik chemiczny, Warszawa 2020.
Oblicz, jaki procent masy otrzymanego roztworu stanowi masa chlorku manganu(II). Załóż, że objętość roztworu się nie zmieniła. Przyjmij wartości mas molowych: MMnCl2 = 126 g∙mol–1 oraz MMnCl2∙4H2O = 198 g ∙ mol–1.